Solving Direct and Inverse Electromagnetic Scattering Problems Using Deep Learning

The Dual Challenge: Forward and Inverse Problems

The thesis focuses on two distinct, yet interconnected, problems in electromagnetics:

• • Forward Problem: This involves predicting the scattered electromagnetic field when the properties of a scattering object (like its shape, size, and composition) and the incident light are known. Traditionally, this requires solving Maxwell’s equations. In this work, the forward problem specifically aims to generate intensity (S₁₁) and linear polarization (LP) data from a given 3D scatterer.

• • Inverse Scattering Problem (ISP): This is the more challenging task. Given measurements of scattered light, the goal is to reconstruct the physical properties, shape, or orientation of the scatterer. ISP is crucial for applications like radar imaging, medical imaging, and nondestructive testing.

Traditional methods for these problems, such as Finite Difference Time Domain (FDTD), Finite Element Methods (FEM), and Method of Moments (MoM), are effective but come with significant computational costs in terms of CPU and memory. Stochastic optimisation methods for ISP also demand large computational resources.

Deep Learning to the Rescue: A Three-Pronged Approach

This thesis proposes a deep learning approach divided into three core sub-tasks, each employing a supervised deep learning strategy:

1. 1. Forward Solver: A convolutional neural network (CNN) architecture, dubbed “F-Net,” is applied to predict the far-scattered field of a given 3-dimensional scatterer.

1. 1. Inverse Problem Solver (Classification): A classifier neural network is used to identify the classes of particle shapes from their light scattering patterns.

1. 1. Shape and Orientation Reconstruction: A method similar to the forward problem’s approach is used to reconstruct the particle’s shape and orientation.

Feature Extraction: Preparing Particles for Neural Networks

To feed 3D particle data into neural networks, efficient feature extraction is vital. The thesis explores two main methods:

• • Occupancy Grid (OCC): This method discretizes the 3D environment into a grid of cells, assigning a binary value (occupied/unoccupied) to each voxel. It effectively captures basic shape information.

• • Signed Distance Field (SDF): SDF represents a particle by calculating the distance from any point in space to the nearest particle surface. This method can characterise particle properties (negative values for inside, positive for outside) and is particularly useful for shape and orientation.

Both methods were employed for the forward and inverse problems, with results indicating their effectiveness in capturing relevant features.

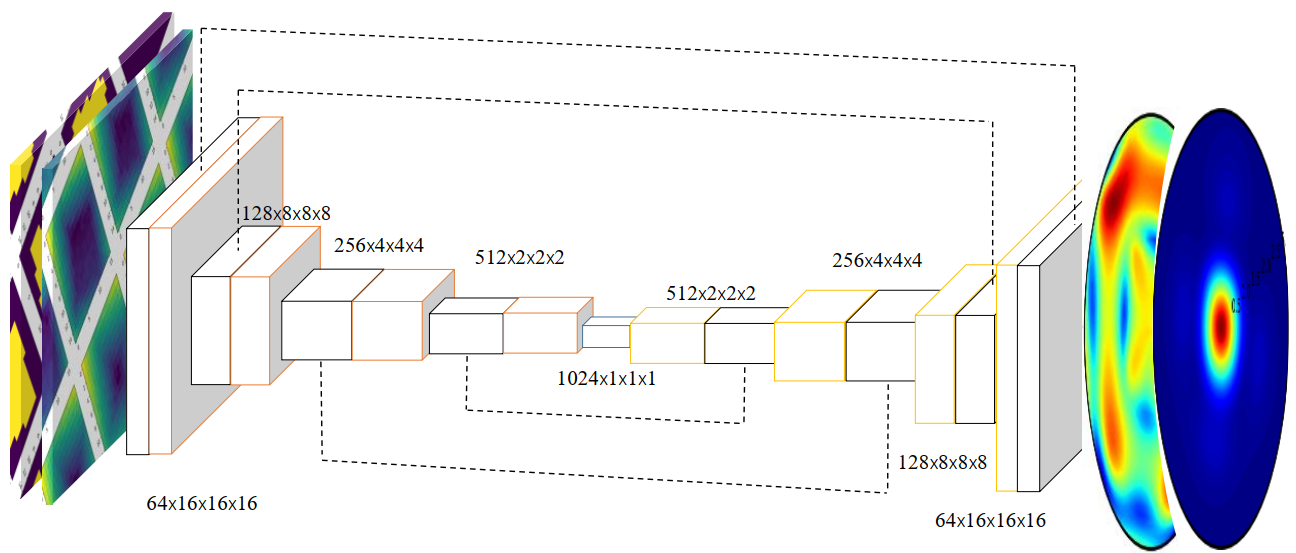
The F-Net: A Fast Forward Solver

The F-Net model is a CNN-based U-net-like architecture designed to predict intensity and linear polarization parameters (S11 and -S21/S11) from Mueller matrices.

• • Architecture: It features contracting and expansive paths with convolutional layers, ReLU activation, and max-pooling, connected by skip connections, leading to a bottleneck layer that captures lower-dimensional data representations.

• • Performance:
    •  
    • • For smaller particles (size parameter x=5), the F-Net showed comparable performance to the traditional ADDA simulator. SDF features generally yielded better results than OCC for both intensity and linear polarization predictions, especially for the latter.
    • • Crucially, the F-Net demonstrated significantly faster computational speeds: approximately 15 times faster for x=5, and up to 50-80 times faster for larger particle sizes (x=10 and x=15), despite some discrepancies at larger parameters. This efficiency makes DNN simulation a promising tool for real-time applications.
    • • However, the network found it challenging to accurately predict intensity values for complex shapes and orientations, especially with larger size parameters (e.g., x=15 for cubic and tetrahedron particles), where prediction errors increased significantly.

Tackling the Inverse Scattering Problem: Classification and Reconstruction

For the ISP, the thesis focused on classifying 10 different particle shapes and reconstructing their 3D forms using scattered light patterns (intensity and LP data from Mueller matrices).

• • Particle Classification:
    •  
    • • Various neural network architectures were tested, including Fully Connected Networks (FCNs), CNNs, and ResNet50 models.
    • • The CNN model generally outperformed FCNs and ResNet50, achieving an accuracy of 81.65% for particle classification using S11 data. This was further improved by using log-transformed input features and the Additive Margin Softmax (ADMS) loss function.
    • • Challenges included class imbalance in the synthetic dataset (e.g., the “egg-shaped” particle) and the inherent predictability of synthetic data, which was addressed by introducing additive noise to enhance generalisation to real-world scenarios.
    • • While promising, the achieved accuracy of 81.65% is noted as lower than a baseline result of approximately 90% from prior research.

• • Shape and Orientation Reconstruction:
    •  
    • • This task involved generating a particle’s property, shape, and orientation from input scattered signals.
    • • A CNN architecture was used, with the intensity or LP data from the Mueller matrix as input.
    • • After the network predicted particle features, the Marching Cubes algorithm was employed to reconstruct the 3D shape.
    • • The results indicated that SDF features provided more useful and accurate shape reconstruction compared to OCC features.

Looking Ahead

This Master’s thesis demonstrates that deep learning can significantly upscale the performance of traditional electromagnetic solvers. The tools developed offer fast solutions to complex problems and show great potential for applications in remote sensing, near-field optics, biology, microscopy, and astrophysics.

Future work could explore 3D modeling based on faces, edges, and vertices, and enhance the feature space by incorporating material properties (like refractive index), internal scatterer structure, and size distribution properties to make the models more relevant for practical applications.

This research marks an exciting step towards more efficient and insightful analysis of electromagnetic scattering phenomena using the power of artificial intelligence.